🎯 Conditional Probability: the silent foundation of Machine Learning
In ML, almost everything boils down to one key idea: calculating the probability of something given that something else happens.
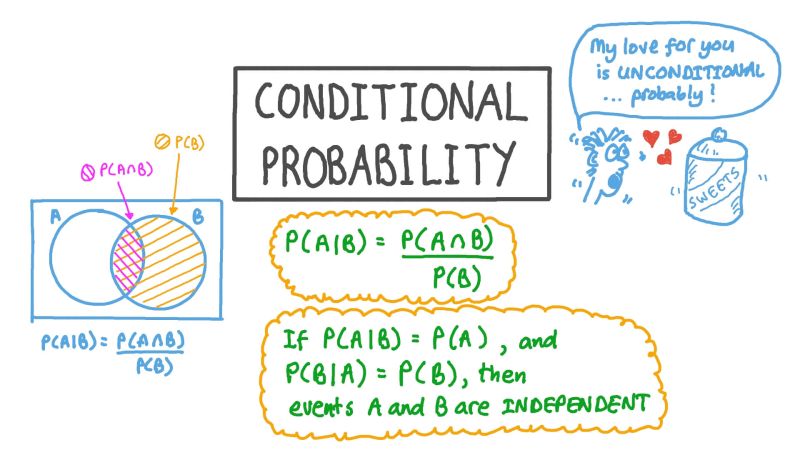
That is conditional probability 👉 $P(A|B)$.
📩 Simple example: spam detection
We want to know: if an email contains “free”, what’s the probability that it’s spam.
For that we need to understand:
- 📊 $P(Spam)$: how often emails are spam
- 🔍 $P(“free”)$: how many emails contain “free”
- 🎯 $P(“free” | Spam)$: how many spam emails include “free”
The last one is what really drives models like Naive Bayes.
🤖 Why does it matter?
- Because all classifiers do this:
- $Recommenders \to ( P(\text{you like an item} \mid \text{your history}) )$
- $Medical\ diagnosis \to ( P(\text{disease} \mid \text{symptoms}) )$
🧠 Think of it as asking: “Given what I already know, how likely is X to occur?”
That question is at the heart of how machines make decisions.
Also published on LinkedIn.
